

Not a member? Sign up now
Question 1
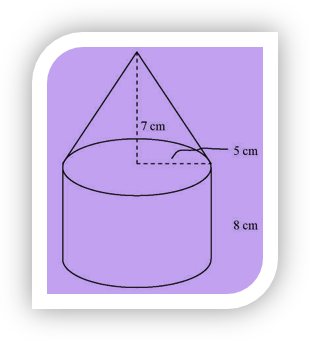
We are given that the object is composed of a cone on top of a cylinder. We can use the Pythagorean relationship to find the slant height of the cone.
Then we can use the formula for the surface of a cone, exculding the bottom .
For the cylindrical part of the object, we can use the formula for the surface area of a cylinder, but only include one circle, the base .
The total surface area can now be calculated:
Therefore the surface area is approximately 465 cm 2 .
To convert the answer to square inches, use 1 cm = 0.3937 in., so 1 cm 2 = (0.3937) 2 in. 2 .
465 (0.3937) 2 = 72.074855
Therefore the surface area is approximately 72 in 2 .
Copyright © 2026, Hold Fast Consultants Inc. No part of this publication may be reproduced in any form or by any means without the prior written permission of Hold Fast Consultants Inc.